
作者: 陈希孺
出版社: 清华大学出版社
出版年: 2000-5
页数: 192
定价: 15.00元
装帧: 平装
丛书: 院士科普书系第一辑
ISBN: 9787302036623
概率——机会大小的度量
机遇、机会、偶然性(随机即随机会而定的意思),在本书讨论的范围内,有同一的意义,指的是一种在事前没有确实的把握,只能在事后见分晓的情况。
机遇或偶然性之所以存在,是由于人类的知识的局限性。
我们讨论只涉及关于偶然性的这样一个方面:虽说由于偶然性的作用,世上的万事万物呈现出一种无序、不可预测以至纷乱的形态,但在这纷乱中,仍有一定的规律性可寻。
本书的主题就是“机遇的数量化”。
古典概率——比率
一般,有n个相异的物件,从其中取出r个进行排列,不同的做法有多少种?用P(n,r)记这个数目,有公式:
P(n,r)=n·(n-1)·(n-2)···(n-r+1) (1)
它利用下述的一般原则:如果办一件事要依次序经过r个环节,而完成第1个环节有n1种不同的办法,完成第2个环节有n2种不同的办法,依次类推,直到完成第r个环节有nr种不同的方法,则办成这件事的不同方法,总共有n1·n2···nr种。
把上述一般原则用于P(n,r)的计算问题。先把“从n物件中取r个去排列”这件事分解成r个环节去办。设物件自左至右排列。先从n物件取1个排在最左边,不同的做法有n种。次一环节是从剩下的n-1个物件中,取1个排在(自左数起)第2位。因只剩下n-1个物件,完成这一环节的不同做法只有n-1。下面再依次取排在第3、第4…到第r位的物件,方法有n-2,n-3,…,n-r+1种。因而不同的排法总数,安上述一般原则,应是n,n-1,…到n-r+1这r个数连乘。
当r=n,按(1)式有:
P(n,n)=n·(n-1)···3·2·1
即最初n个正整数连乘,其结果称为n的“阶乘”,记为n!。
组合数:从n个相异物件中取r个组合,其不同做法的总数C(n,r):
C(n,r)=P(n,r)/r!=n·(n-1)···(n-r+1)/r! (2)
每一个由r物件构成的组合,可以通过将这r物件任意排列,其数目按刚才的论证为r!。因此,排列数P(n,r)应为组合数C(n,r)的r!倍。
基于试验结果的等可能性,用公式P(A) = M / N规定的概率,叫做“古典概率”。
大数定律
说到底,从现实世界的角度看,大数定律是人类观察到的一个经验规律。伯努利大数定律(及其他形形色色的大数定律)的意义,在于对这样一个经验规律给了一个理论上的解释。
统计概率——频率
设观察了n次而事件A出现了m次,m/n称为事件A的频率。我们相信,当n愈来愈大时,频率m/n随有些摆动,但幅度愈来愈小而最终会“趋近”于某一介于0与1之间的值p,就把这个p定义为事件A的概率。用这种方式定义的概率叫做“统计概率”,因为它是通过“统计”(即进行观察)去定义概率的。
在古典概率的场合,事件概率有一个不依赖于概率的定义——它根本不用诉诸试验,这样才有一个频率与概率是否接近的问题,其研究导致伯努利大数定律。在统计定义的场合这是一个悖论:你如不从承认大数定律出发,概率就无法定义,因而谈不上频率与概率接近的问题。但如你承认大数定律,以便可以定义概率,那大数定律就是你的前提,而不是一个再需要证明的论断了。
在平面几何中,像“过两点有一条且只有一条直线”、“过直线外一点有一条且只有一条与此直线平行的直线”等,就是作为不加证明而接受的公理。在1933年,前苏联数学家柯尔莫哥洛夫把这种公理化的思想用到概率上。从几条简单的公理出发,推导出其他内容。
主观概率
这种基于主观判断定出的概率,叫做“主观概率”。主观概率是认识主体根据其所掌握的知识、信息和证据,而对某种情况出现可能性大小所做的数量判断。
概率分布
概率分布中 “分布”一词的意思是:它指明全部概率是1是如何分布到(分配到)随机变量x的各个可能值的。
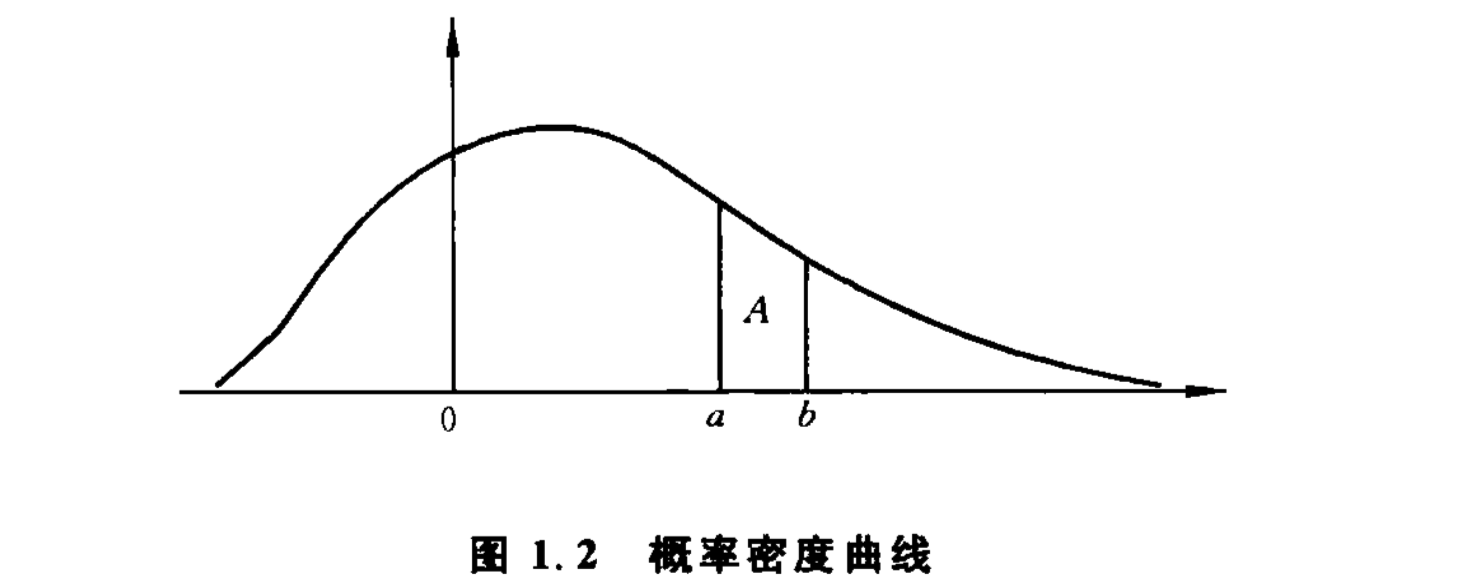
对于连续型的随机变量,我们不采取逐一列举其概率的办法,而是设法定出如图1.2那样一条曲线,称为概率密度曲线。此曲线位于一条横轴的上方,它与横轴一起所谓成的面积为1,而变量落在指定的两个数a和b之间的概率,就是图中用字母A标出的那一块条形的面积。
期望与方差
期望及其意义
一般,如果随机变量x能够取的值是 $a_1,a_2,\cdots,a_r$,取这些值的概率为 $p_1,p_2,\cdots,p_r$,则把
$E(x)=a_1p_1+a_2p_2+…+a_rp_r\ (4)$
称为x的期望。如果对x做大量次数的观察,则由于偶然性的影响,x的各次取值将呈现出一个很纷乱的状态,但其中有规律性在,即随着观察次数的增加,其平均取值的波动愈来愈小,最后稳定到一个值,此值即x的期望。从这个解释可以看出:期望的意义要在大量重复观察中才能体现出来。
切比雪夫大数定律
“关于期望值的大数定律”:对一个随机变量进行多次观察,其各次取值的平均愈来愈接近它的期望值。这个定律最初是由俄国数学家切比雪夫在19世纪中叶首先提出,故常称为切比雪夫大数定律。到20世纪30年代,苏联数学家柯尔莫哥洛夫给了这个定律以一个更完备的形式,称为柯尔莫哥洛夫大数定律。
标准差的误差估计
设有一个很大的群体,其个体的某项指标x(如人的身高)在全群体中的平均值a未知,通过从该群体中抽得的若干个体的数值 $x_1,x_2,\cdots,x_n$ (如抽出的n个人的身高)去估计它,从大数定律可知,$x_1,x_2,\cdots,x_n$ 的算术平均:
$\bar{x}=\frac{x_1+x_2+\cdots+x_n}{n}\ (7)$
是一个合用的估计。当抽取观察的个体数n增加时,估计的误差会下降,理论上可以证明,总得讲 误差随$\sqrt{n}$成比例下降。 例如,$\sqrt{16}=4,\sqrt{144}=12$。因此按上述规律,若甲的观察数为16而乙的观察数为144,则总得讲,甲所作估计的误差将是乙所作估计的误差的3倍。
这个规律的确切解释用到标准差。如上所述,x的标准差σ(x),反映x与其均值a偏离的程度,这是一个综合性的指标。如果对x观察n次得$x_1,x_2,\cdots,x_n$,而按(7)式计算其算术平均$\bar{x}$,则可以证明:$\bar{x}$的标准差$\sigma(\bar{x})$缩减到原来的$\sqrt{n}$分之一:
$\sigma(\bar{x})=\frac{\sigma(x)}{\sqrt{n}}$
正态分布标准差
正态分布依赖两个参数μ和σ。μ就是分布的均值。σ的值决定了曲线的陡峭程度:σ愈小,曲线愈陡峭,而这又意味着分布的集中度高。σ就是分布的标准差。正态分布用$N(\mu,\sigma^2)$来记。
在正态分布的情况下,用n个观察值的算术平均$\bar{x}$去估计期望μ,其所产生的误差与标准差σ和n的关系,有一个简单的描述,那就是,“$\bar{x}$与μ的差距不超过$c \cdot \frac{\sigma}{\sqrt{n}}$”的概率,即:
$P_c=P(-c \cdot \frac{\sigma}{\sqrt{n}} \le \bar{x}-\mu \le c \cdot \frac{\sigma}{\sqrt{n}})\ (8)$
用$P_c$这么大的概率保证:虽然$\bar{x}$不大可能恰好等于要估计的μ,但它与μ的差距很可能不会超过$c \cdot \frac{\sigma}{\sqrt{n}}$。(8)式中的$P_c$的值依赖于c,可以从专门制备的“正态分布表”上查到。例如:
$p_{1.6449}=0.90, p_{1.9600}=0.95, p_{2.5758}=0.99$
公式(8)在实用上有多方面的用途,举一个例子,在应用上有时我们会面临如何决定n的问题。n定得太小,则用$\bar{x}$去估计μ可能产生过大的误差。反之,若n定得太大,则会造成不必要的浪费。如何确定n,要根据对估计的质量的要求。比如说,要求以0.95的概率保证$\bar{x}$与μ的差距不超过0.5,因为$p_{1.96}=0.95$,按(8)式,这等于要求:
$(1.96)\frac{\sigma}{\sqrt{n}}=0.5$
或
$n=\frac{(1.96\sigma^2)}{(0.5)^2}=(15.3664) \cdot \sigma^2$
如果此数不是整数,则以其邻近而大于它的整数取代之。例如算出的结果为17.3565,则用18取代。这个解法要求已知σ的值。
观察次数n与用$\bar{x}$去估计μ的误差之间的关系——平方根比律,在历史上首先是由法国概率论学者棣莫弗在1733年发现的。
这个规律反映了一种“报酬递减”的性质:随着观察次数的加大,每再增加一次观察的收益(体现在用$\bar{x}$估计μ的误差的下降上)减少:观察400次而做出的估计所产生的误差,较之观察100次而做出的估计所产生的误差,只缩小了一半。换句话说,后300次观察(在前100次观察的基础上)的效益,与前100次观察同。这告诉我们:一味追求加大观察次数是无益的。
统计学——收集和分析数据的学问
什么是统计学
用实证的方法研究问题,都要涉及收集数据以及对数据进行整理和分析,统计学就是研究做这些事情的方法和理论的学问。
统计学是有关收集和分析带随机性误差的数据的科学和艺术。分析着重在数理化,而随机性的数量化,是通过概率表现出来,由此可以看出统计学与概率论的密切关系。大体上,二者的关系是:概率论是统计学的理论和方法的依据,而统计学可视为概率论的一种应用。
从部分推整体:归纳与演绎
统计方法是一种归纳性质的方法,统计推断是一种归纳推理。
统计规律与因果关系
“统计规律”这个提法的启示是:教人看问题不可绝对化,因而有思想方法上的教育意义。习惯于从统计规律看问题的人在思想上不拘执一端:他既认识到一种事物从总的方面看有其一定的规律在,也承认存在例外的个案。
从反面讲,也可以说统计规律这种东西的出现,反映了人类认识上的局限性,反映了人类对偶然性的作用无力完全掌握,也反映了人类在这种局限性的约束下认识自然的一种努力,即在偶然性造成的纷乱无序的状态下,尽量从中找出一些虽不完善,但具有规律性的品格的东西。
其次,统计方法只是从事物的外在数量表现上去研究问题,通过对数据的分析,揭示可能有某种规律性的东西存在,而不涉及事物的质的规定性。换句话说,统计分析的结果可以告诉你,从观察和试验资料来看事情是怎样的,而不能告诉你为什么为这样。
应当指出的是:统计规律未必蕴含因果关系,这一点,是统计方法的本性而非缺陷。寻找因果关系是各类专门学科的任务。
抽样调查
简短的历史
随机抽样归结到一个基点:要求群体中的每一个体有同等机会(概率)被抽出,这样,哪一个体进入样本,纯由机会确定。
每一项抽样调查,都应附有对所有抽样方法的仔细陈述。若没有这样的陈述,研究的结论的可靠性和精度就无从评估。
抽样的方法
这种将样本的选定委之于机会的抽样,叫做随机抽样。随机抽样方法把调查对象的选定委之于机会,目的是为了避免调查者主观上的偏向性。
数据的分析(区间估计与点估计)
以下几个问题及研究处理方法是典型的:
- 总体分布
- 总体平均值
- 总体方差
- 总体均值的估计:样本均值
- 总体方差的估计:样本方差
$\tilde{\Delta}^2=\frac{N-1}{(n-1)N}\sum_{i=1}^n(x_i-\bar{x})^2\ (13)$
其中N是总体所含个体数。$\tilde{\Delta}^2$是修正的样本方差,它是$\sigma^2$的无偏估计。
作为抽样的目的,主要是为估计总体平均值a,其所以估计总体方差$\sigma^2$,在很多情况下,是为了由此评估用样本均值$\bar{x}$估计a的精度如何。
a的值界于$\bar{x}-h\frac{\tilde{\Delta}}{\sqrt{n}}$与$\bar{x}+h\frac{\tilde{\Delta}}{\sqrt{n}}$之间(14)
其中$\tilde{\Delta}$由(13)式算出,n为样本量。h是一个选定的大于0的数。从(14)看出:1)$\tilde{\Delta}$愈小,此界限愈窄,表明以$\bar{x}$估计a的误差小。$\tilde{\Delta}^2$是作为总体方差σ2的估计。权且认为$\tilde{\Delta}$大体上为σ,σ愈大,总体中各个值的指标散布也大,在这种情况下,总体均值a就难得估准,反映在(14)式中,a的误差界限就大一些;2)$\sqrt{n}$在分母,故n愈大,(14)式规定的界限愈窄。
h取得愈大,由(14)定的界愈宽。它真能成立的可能性就更大。正如估计人的年龄,估计他在30 ~ 31岁之间,成立的可能性不大,若估计他在10 ~ 80之间,则可能性大多了。由此可见,a的选择面临一个“可靠性”与“准确性”的矛盾问题:把事情说得太确切,不留余地,可靠性就低;说得稀松一些,留有余地,可靠性就搞。在应用上选择a时是在这二者之间做出适当的折衷,看哪个因素更要紧一些。在统计学上比较常用:
h=2.5758,相应于可靠度99%;
h=1.9600,相应于可靠度95%;
h=1.6449,相应于可靠度90%。
像(14)这样的断语,称为a的“区间估计”,相应地,像“用$\bar{x}$估计a”称为a的“点估计”。
通过试验收集数据
试验需要设计
干扰一个试验结果的有:(1)混入的系统性因素。(2)随机性的误差。前者是指那种显著的,可以造成重大错误的因素,例如病人的情况不同可能对疗效的估计产生重大错误。又如要通过试验验证,一种工业产品的新配方(或新工艺),是否真能改善产品的性能。但新旧两种配方的试验分在两个工厂做,而这两个工厂的设备条件和工人素质都有差异,后者作为系统性因素混入试验结果,使我们无法做出可信的结论。随机性因素的影响是不可能完全消除的,只能采取一些办法加以抑制。
双盲试验
比如某厂试验了一种新药,要通过临床试验鉴定其疗效如何。首先,要预备一种表面上看与药物完全一样,但不含任何疗效成分的安慰剂。其次,要设对照组,即准备服用安慰剂的一组病人。受试的病人编入治疗组或对照组按随机的方式决定,以免由于偏向而将条件好的病人多分入某一组。第三,参加试验的病人并不知道他分在哪一组,给药的医生以及评估疗效的医生也不知道谁分在哪一组,以及谁吃了药还是安慰剂。这样,无论是病人自己还是参加试验的医生,都处在盲目的状态中,不致因心理作用或态度上的偏向而干扰试验结果。
单因素试验
试验有一定的目标。例如,一个农业试验的目标,可以是为了比较3个小麦品种的优劣。3个小麦品种是我们要比较的对象。我们把“品种”称为问题中的一个“因素”或“因子”,本试验要比较的对象只有品种一个因素,在统计学上称为“单因素试验”,如果试验的目的还包括比较几种肥料的优劣,则是一个2因素试验。
3个小麦品种,是这个因素的一个水平,故总共有3个水平。
设计试验的下一步骤,是要确定每个水平的“重复度”,就是准备拿每个水平做多少次试验。
多因素试验
多因素试验是指在同一个试验中,影响目标值的因素有2个或2个以上,且这些因素的作用都在试验考察的范围内。一个简单的例子,设有两个种子品种A和B,两个播种量a和b,按复合试验,有4个组合要做试验:
Aa,Ab,Ba,Bb
每一个可能的组合,例如Ab,称为一个“处理”。本试验共有2个因素,每因素各有2水平,处理总数是所有可能的组合数,即
处理总数=各因素的水平数的乘积(2 x 2 = 4)
数据的统计分析——机会限度的认识
显著性检验
“女士品茶”:一种饮料由牛奶(milk)和茶(tea)混合而成,调制时可以先倒茶后倒牛奶(TM),也可以先倒牛奶后倒茶(MT)。有一位女士说她能分辨(鉴别)此二者。费歇尔设计了一个试验来检验该女士的说法是否确实。试验的布置是:准备8杯看上去一样的饮料,其中TM和MT各4杯,把这一点告诉该女士(但不指出哪4杯是TM),然后让她品尝这8杯饮料,指出哪4杯是TM。根据她的回答来估量她是否确有分辨TM和MT的能力。
从8杯中挑出4杯的不同挑法有:$C(8,4)=\frac{8 \cdot 7 \cdot 6 \cdot 5}{1 \cdot 2 \cdot 3 \cdot 4}=70$
其中只有一种是全部条对,其可能性(概率)只有1/70。因此,在“该女士4杯全部挑对”这个试验结果出现时,只有两种可能的解释:
- 该女士对TM和MT并无鉴别能力,所得结果纯属偶然。
- 该女士对TM和MT有一定的鉴别力。
按上面的计算,若坚持第一种解释,则我们就得承认:发生了一件其概率只有1/70的事情。由于1/70相当小,这看上去不大可信,因而我们摒弃这一解释而接受第二种解释。结论:试验结果支持“该女士对TM和MT有一定鉴别力”的说法。
费歇尔的推理中包含以下几个要点:
- 问题是要辨明试验结果是否支持某种效应(例如,能分辨TM和MT)。
- 把“效应不存在”作为一个“假设”(假设该女士对TM和MT无鉴别力)。
- 找一个显示试验结果与假设之间的偏差的量,在“假设正确”的前提下,计算出现这么大偏差的概率p。
- 如果p小到某个程度,以至认为发生概率那么小的事件为不可信,则认为数据没有给假设以足够的支持,或反过来说,数据支持“效应存在”的说法。反之,若p并非足够小,则数据没有给予“否定假设”以足够的支持。
费歇尔把这种性质的推理叫做“显著性检验”。显著程度是用概率来表示,概率愈小,显著性愈高,肯定效应存在的理由就愈充足。
一般指定阈值为0.05或0.01,称其为“显著性水平”。
拟合优度检验
有一随机变量x,根据某种理论,其分布表应为:
(3):
| x的取值 | a1 | a2 | … ak |
|---|---|---|---|
| 事故概率 | p1 | p2 | … pk |
为检验这是否正确,对x进行n次观察,发现其取a1,a2,…,ak等值的次数分别为n1,n2,…,nk。问这一结果与分布表(3)拟合的程度如何。
皮尔逊处理这个问题的想法是:找一个反映数据与假设的偏差的量D,D愈小,数据与假设之间的拟合就愈好。按一定的方法把D值转换成一个概率p(D)。p(D)的意思可以确切地解释为:即使假设正确,但由于观察结果受到偶然性的影响,数据与假设之间也会呈现一定的偏差。偏差大到或超过D这样的限度的概率,就是p(D)。p(D)愈大,就表明发现像D这么大的偏差不算稀奇,而我们就认为观察数据与假设拟合得比较好。如果p(D)很小,就表明:所发现的偏差,仅从观察结果受到偶然影响这方面去解释就比较牵强。因此,把概率p(D)称为(数据与假设之间的)拟合优度。如果要求一个黑白分明的判定,则可以定下一个阈值,例如0.05,0.01之类,当p(D)小于此阈值时,就否定假设。这与费歇尔的显著性检验一样,此阈值也就是检验的水平。
设一共观察了n次,因为X取a1为值的概率为p1,平均讲在n次观察中X应有np1次值a1,而真实观察的取a1的次数为n1,对每个值a1,a2,…,ak依次类推,算出D:
$D=\frac{(n_1-np_1)^2}{np_1}+=\frac{(n_2-np_2)^2}{np_2}+…+=\frac{(n_k-np_k)^2}{np_k}\ (4)$
称为皮尔逊统计量。
表5.1 对应于阈值0.05和0.01的D值
| 阈值\k | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
| 0.05 | 3.841 | 5.991 | 7.815 | 9.488 | 11.070 | 12.592 | 14.067 | 15.507 |
| 0.01 | 6.635 | 9.210 | 11.341 | 13.277 | 15.086 | 16.812 | 18.475 | 20.090 |
表中所列的,就是相应于某个k(k就是(3)中的那个k)和阈值的D值。若由数据算出的D值超过表中的值,则认为观察数据与假设的偏差,已大到不能仅用偶然性去解释的地步,而决定否定原假设。若D不超过表中的值,则认为偏差尚未大到不可用偶然性去解释的程度,而维持这个假设。
用皮尔逊的方法来处理前面的例子。在工厂事故的例中,k=3,n1=6,n2=3,n3=6,n=n1+n2+n3=15,p1=p2=p3=1/3,代入(4)得D值为:
$D=\frac{(6-5)^2+(3-5)^2+(6-5)^2}{5}=\frac{6}{5}=1.2$
此值小于表5.1中k=3所对应的D值。因此,在0.05的水平上,数据没有给“各班次发生事故的机会有差异”这个说法以足够的支持。
相关与相关系数
以X,Y记一对变量,对它们进行了n次观察,结果为(x1,y1),(x2,y2),…,(xn,yn)。
$\Delta_x=\sqrt{\sum_{i=1}^n(x_i-\bar{x})^2}\ (5)$
$x_1’=(x_1-\bar{x})/\Delta_x,$
$x_2’=(x_2-\bar{x})/\Delta_x,$
$\cdots$
$x_n’=(x_n-\bar{x})/\Delta_x,$
$y_1’=(y_1-\bar{y})/\Delta_y,$
$y_2’=(y_2-\bar{y})/\Delta_y,$
$\cdots$
$y_n’=(y_n-\bar{y})/\Delta_y.$
$\Delta_y=\sqrt{\sum_{i=1}^n(y_i-\bar{y})^2}\ (6)$
$r=x_1’y_1’+x_2’y_2’+…+x_n’y_n’\ (7)$
r就是相关系数。以上讲的是有了样本如何计算相关系数。因r是由样本计算所得,故常称为“样本相关系数”。但样本只是总体的一部分,它受到偶然性的影响,故样本相关系数r中包含了偶然的成分。
总体相关系数𝞺(理论相关系数)才确切反映相关的程度。r仅是𝞺的一个估计。它的误差与样本量n有关:n愈大,误差愈小。
表5.2 相关系数的0.05界限值
| 样本量 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|
| 界限值 | 0.63 | 0.42 | 0.35 | 0.30 | 0.27 | 0.25 | 0.23 | 0.22 | 0.21 | 0.19 |
| 例如,你抽的样本有10个,则算出的样本相关系数绝对值 | r | 必须大于0.63,才能否定𝞺=0的假设。而如果样本量为100,则 | r | 只须大于0.19就行。 |
回归方程
对于x,y的回归方程式,x,y之间无严格的关系,这方程也不是对群体中任一个样本都对,而是在平均意义上,或者说,它用一个简练的形式总括了x,y之间的复杂关系的大趋势。