概率
概率介绍
在可能出现几种不同的结果的情况下,对于任一种特定结果的概率被定义为所有可能结果的分数或比例。如果将可能的结果表示为A、B、C、D等,那么:
A的概率=结果为A的个数/可能的结果的总数
一个随机样本要求在总体中的每个个体都有相等的机会被选择。对于许多统计公式都是必要的第二个要求是,如果选择不止这个个体,选择这个个体的概率与选择另一个个体的概率必须相同。
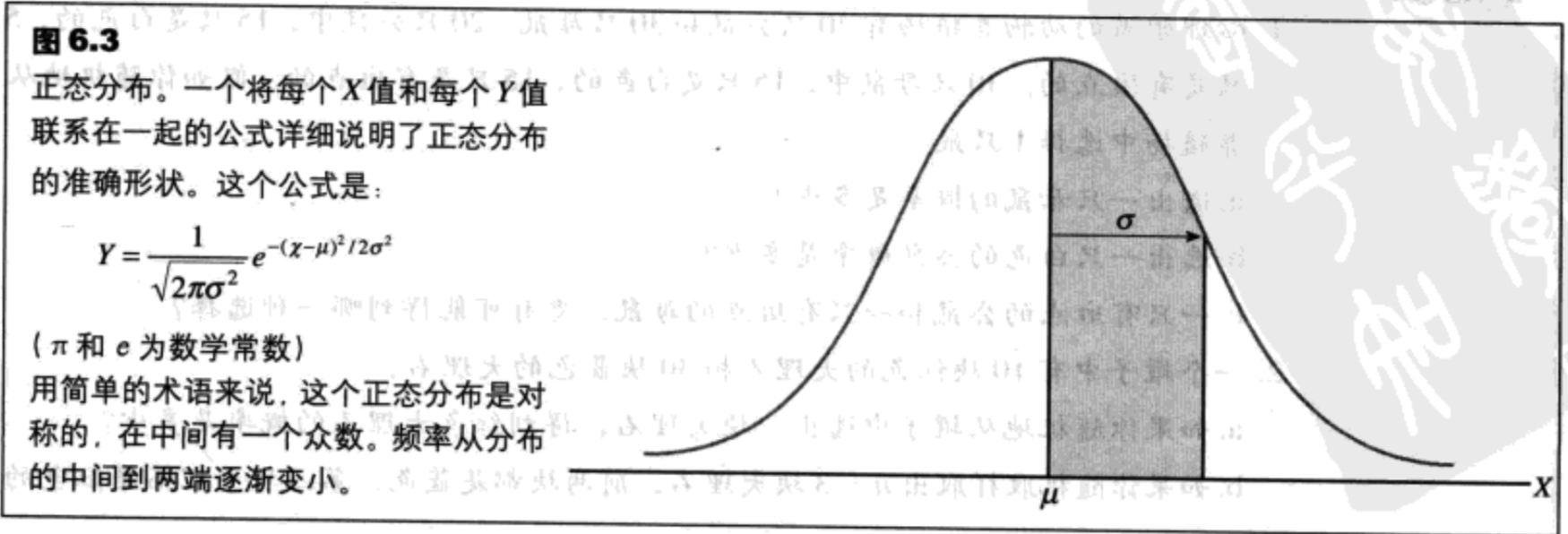
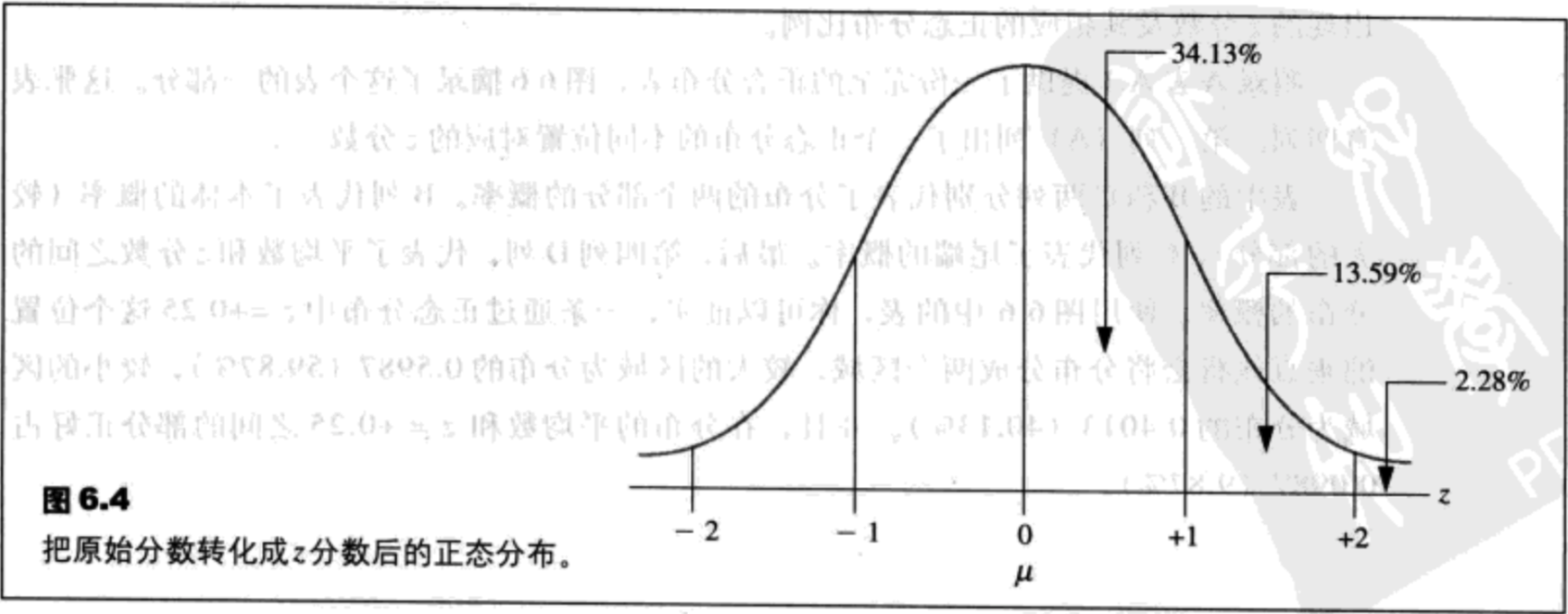
概率与正态分布
概率与二项分布
二项分布
- 两个类别被记做A和B。
- 与每个类别相应的概率(或比例)被记做:
- p=p(A)=A的概率
- q=p(B)=B的概率
- p+q=1.00
- 样本的个体或观察的个体被记做n。
- 变量X指类别A在样本中出现的次数。
使用这个记号法,二项分布显示了与从X=0到X=n的每个X值相应的概率。
二项分布的正态近似
当n较大时,二项分布倾向于趋近正态分布。具体来说,pn和qn都大于等于10的时候,二项分布将会是一个近似的正态分布:
平均数:$\mu=pn\ (6.1)$
标准差:$\sigma=\sqrt{npq}\ (6.2)$
$z=\frac{X-\mu}{\sigma}=\frac{X-pn}{\sqrt{pqn}}\ (6.3)$

关于推论统计
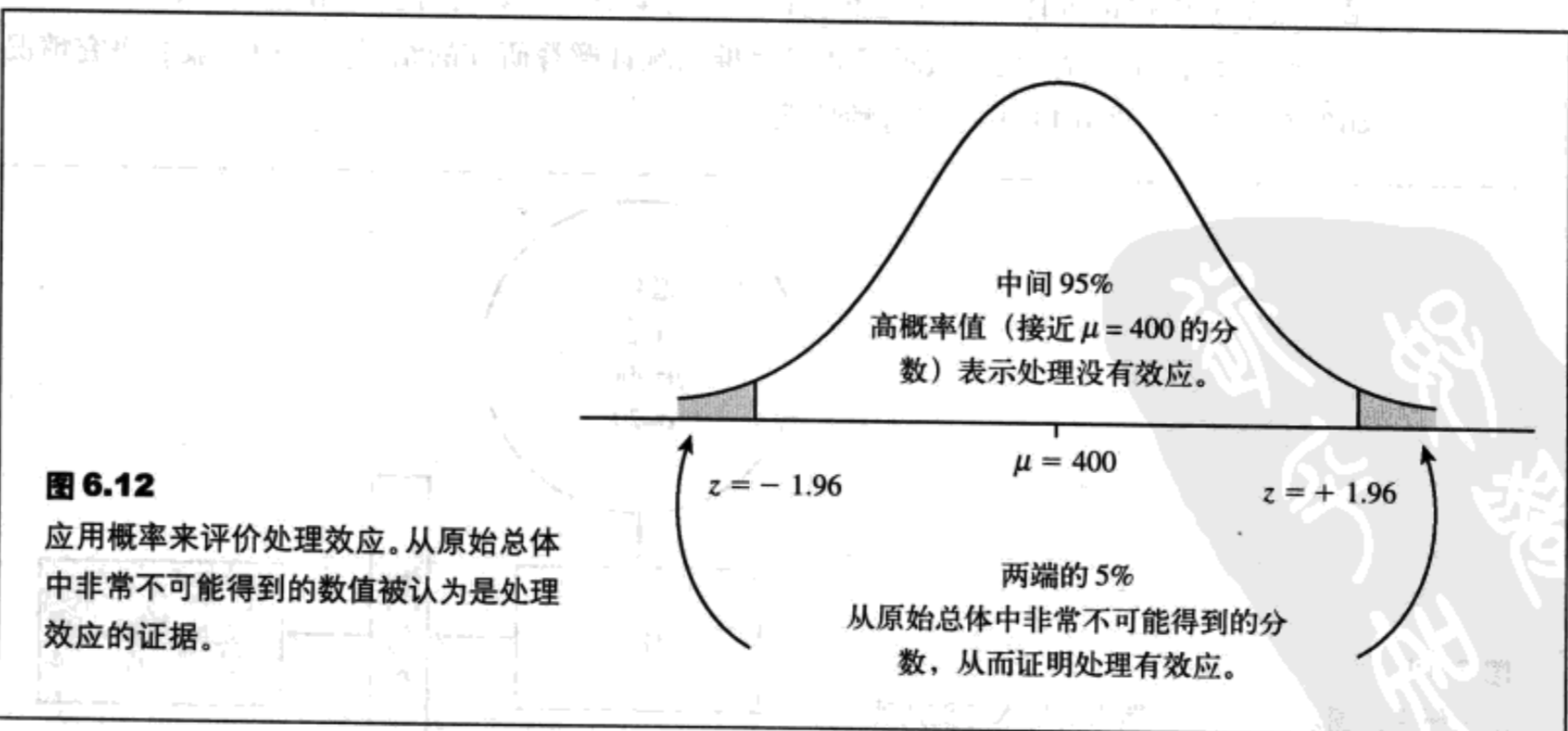
图6.12所示为来自我们的假设研究的最初总体。注意大部分的分数位于μ=400附近。另外还需注意,我们已经分布的中央95%与极端的5%分开的界限。边界位于z=+1.96和z=-1.96处(右尾端极端值0.025的边界为z=+1.96,左尾端极端值0.025的边界为z=-1.96。这两个尾端合计占分布的0.05)。
边界被设定在z=±1.96,这决定了样本是否与原始的总体显著不同的客观标准。具体来说,一个落在超过z=±1.96的边界以外的样本不只是极端值,它也极端地不可能出现,这里“极端地不可能”被定义为小于等于5%的概率。