t分数
t分数——代替z分数的一种方法
大多数情况下,总体的标准差是未知的。在这种情况下,就不能计算标准误,也就不能计算假设检验的z分数。这里介绍一种新方法,叫做t分数。
样本方差=$s^2=\frac{SS}{n-1}=\frac{SS}{df}$
样本标准差=$s=\sqrt{\frac{SS}{n-1}}=\sqrt{\frac{SS}{df}}$
标准误=$\sigma_M=\frac{\sigma}{\sqrt{n}}=\sqrt{\frac{\sigma^2}{n}}$
估计标准误=$s_M=\frac{s}{\sqrt{n}}\ (9.1)$
注意,M的估计标准误的符号是$s_M$,而不是$\sigma_M$。这表明,估计值只是从样本数据得来的,而不是从真正的总体参数得来的。
当σ值未知时,估计标准误($s_M$)被用作对实际标准误$\sigma_M$的估计值。估计标准误是从样本方差或是样本标准差计算出来的。他提供了一个从样本平均数M到其总体平均数μ之间的标准距离的估计。
$t=\frac{M-\mu}{s_M}\ (9.2)$
当σ值未知时,t分数是用来检验有关未知总体平均数μ的假设。除了t分数用估计标准误做分母外,t分数的公式与z分数的公式结构相同。
自由度
自由度是指在样本中有多少个分数是独立的,并可以自由地变化。因为样本平均数限制了一个样本分数的值,这个样本的自由度是n-1。
自由度=df=n-1 (9.3)
一个样本的df值越大,$s^2$就能越好地代表$\sigma^2$,t分数也就更加接近z分数。显然,样本分数个数越多,样本就能更好地代表总体。因此,自由度与s2联系在一起,同时描述了t代表z的程度。

假设检验和t分数
t = 样本平均数(从数据中算出)- 总体平均数(从$H_0$的假设得出) / 估计标准误(从样本数据中算出)
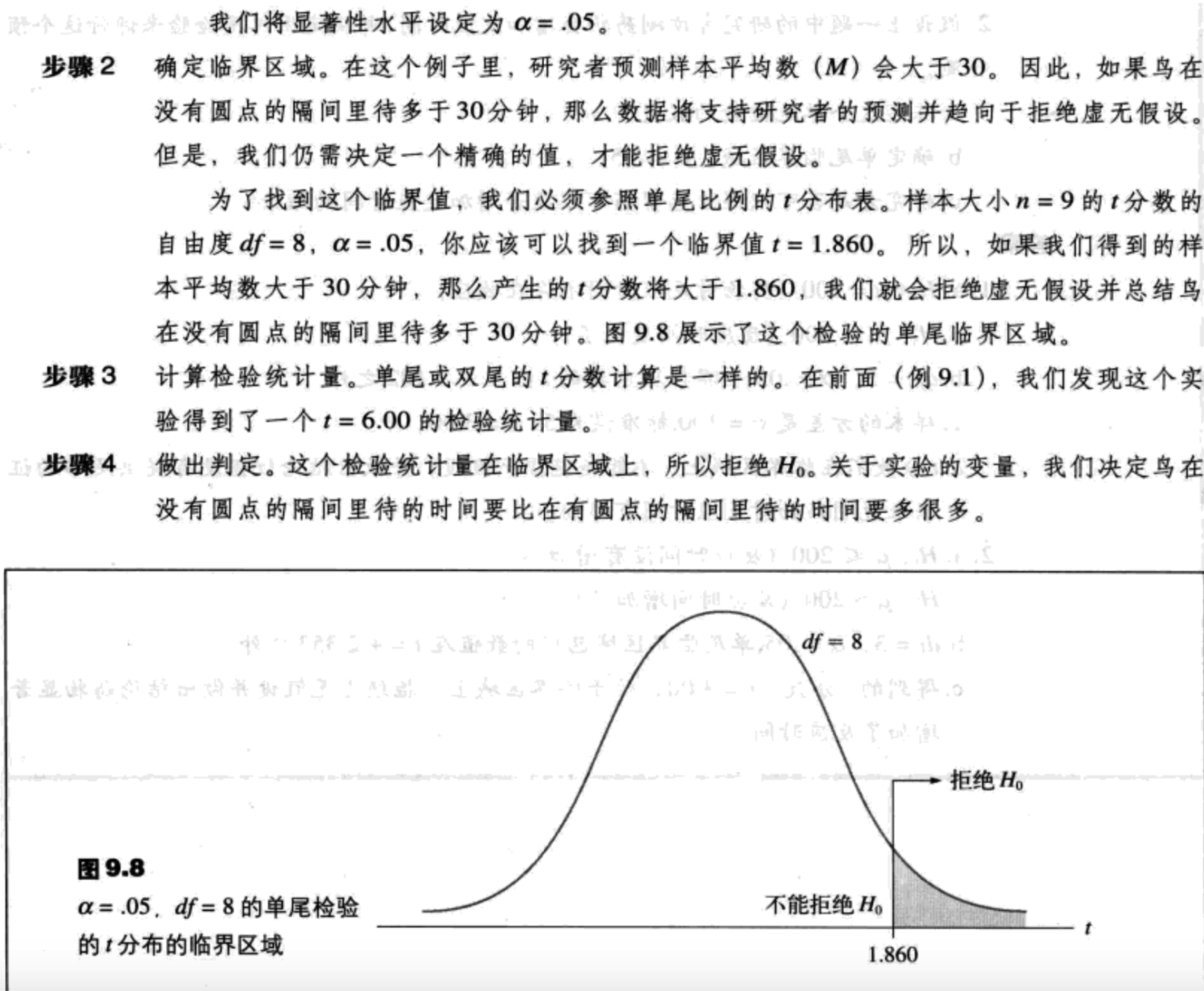
过程与步骤
- 陈述假设,确定$\alpha$水平。虚无假设了陈述处理不存在效应;总体平均数没有变化。备择假设陈述处理存在效应。这两个假设的陈述都包含未知的总体参数$\mu$。
- 确定临界区域的位置。t分布的准确形状与随自由度变化而变化的临界t值。确定df值对于在t分布中找到临界区域是必要的。临界区域可以通过参考t分布表来确定。
- 收集样本数据,计算检验统计量。当$\sigma^2$未知时,检验统计量就是t分数(公式9.2)。
- 对虚无假设做出判定。当我们在步骤3中得到的t分数落在临界区域里(超过了临界t值),于是$H_0$被拒绝。我们可以得出,存在处理效应。但是,如果得到的t值没有落在临界区域上,那么,我们就不能拒绝$H_0$,于是得出结论,在我们的研究中没有有关处理效应存在的证据。
假设检验的例子
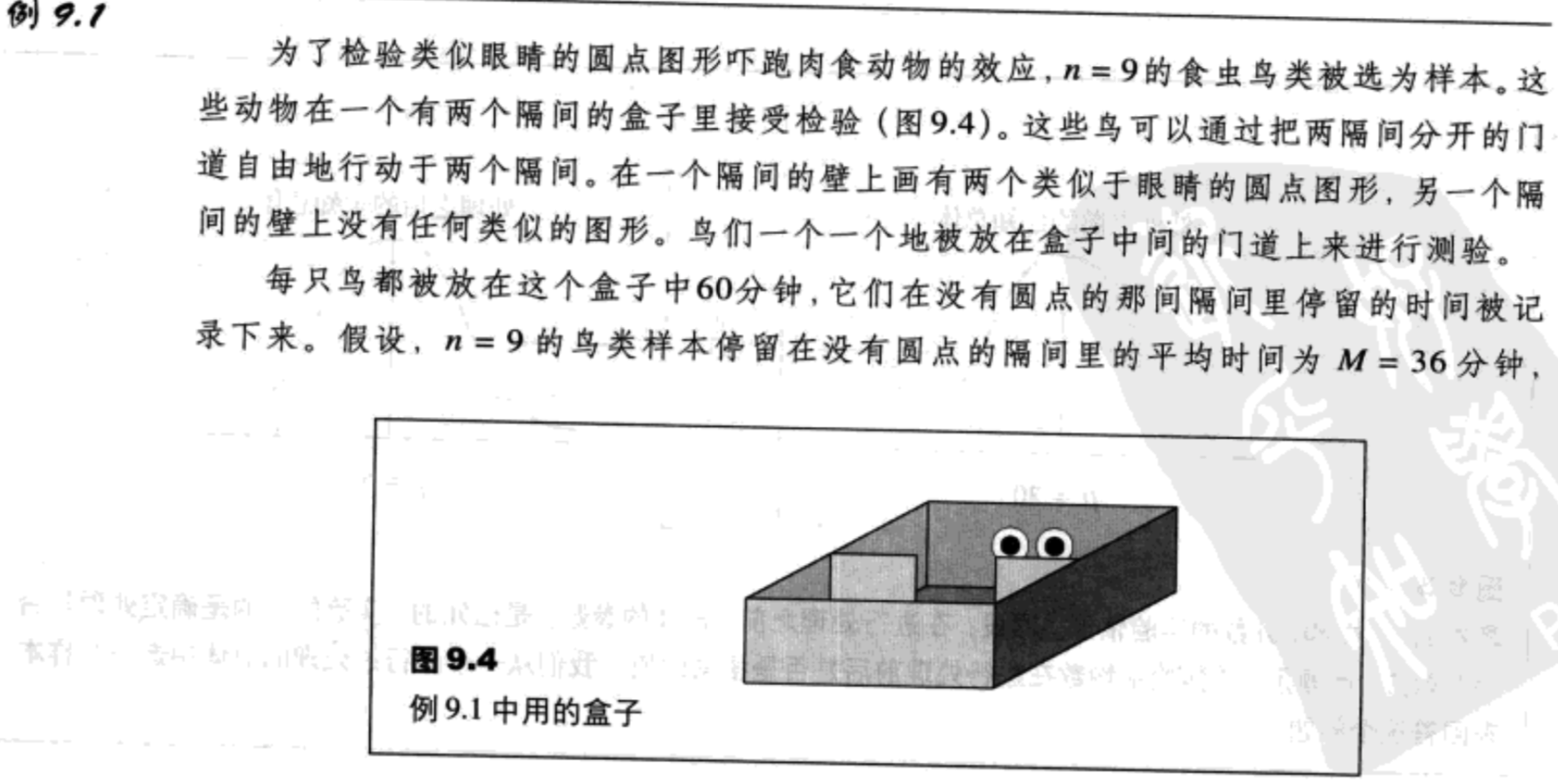


有关t检验的假设
对于t分数的假设检验必需的两个基本的假定为:
- 样本中的数值必须包含互相独立的观察。
- 样本来自的总体必须是正态分布。
t检验中效应大小的测量
估算科恩d值
首次介绍科恩d值时,公式:科恩d值=平均数差 / 标准差
估计科恩d值的公式变成:估计的科恩d值=平均数差 / 样本标准差 (9.4)

$r^2$值
$r^2=\frac{t^2}{t^2+df}\ (9.5)$
从例9.1的假设检验中我们得出当df=8时,t=6.00。这些数值产生:
$r^2=\frac{6^2}{6^2+8}=0.8182$(或81.82%)
注意,这个值与直接计算由处理引起的变异性的百分比是相同的。
解释$r^2$ 除了发展科恩d值来测量效应大小,科恩(1981)还提出评估由$r^2$测量的处理效应大小的标准。实际上,这些标准是建议用来测量相关大小的r,但是,很容易就被扩展应用带$r^2$。用来解释的$r^2$标准列在了表9.3中。
根据这些标准,例9.1、9.2中的数据展示了非常大的效应$r^2=.8182$
表9.3 科恩(1988)提出的用来解释$r^2$值得标准
| $r^2$值 | 效应 |
|---|---|
| 0.01<$r^2$<0.09 | 小效应 |
| 0.09<$r^2$<0.25 | 中等效应 |
| $r^2$>0.25 | 大效应 |
方向性假设与单尾检验