第九章 方差分析及回归分析
1 单因素试验的方差分析
(一)单因素试验
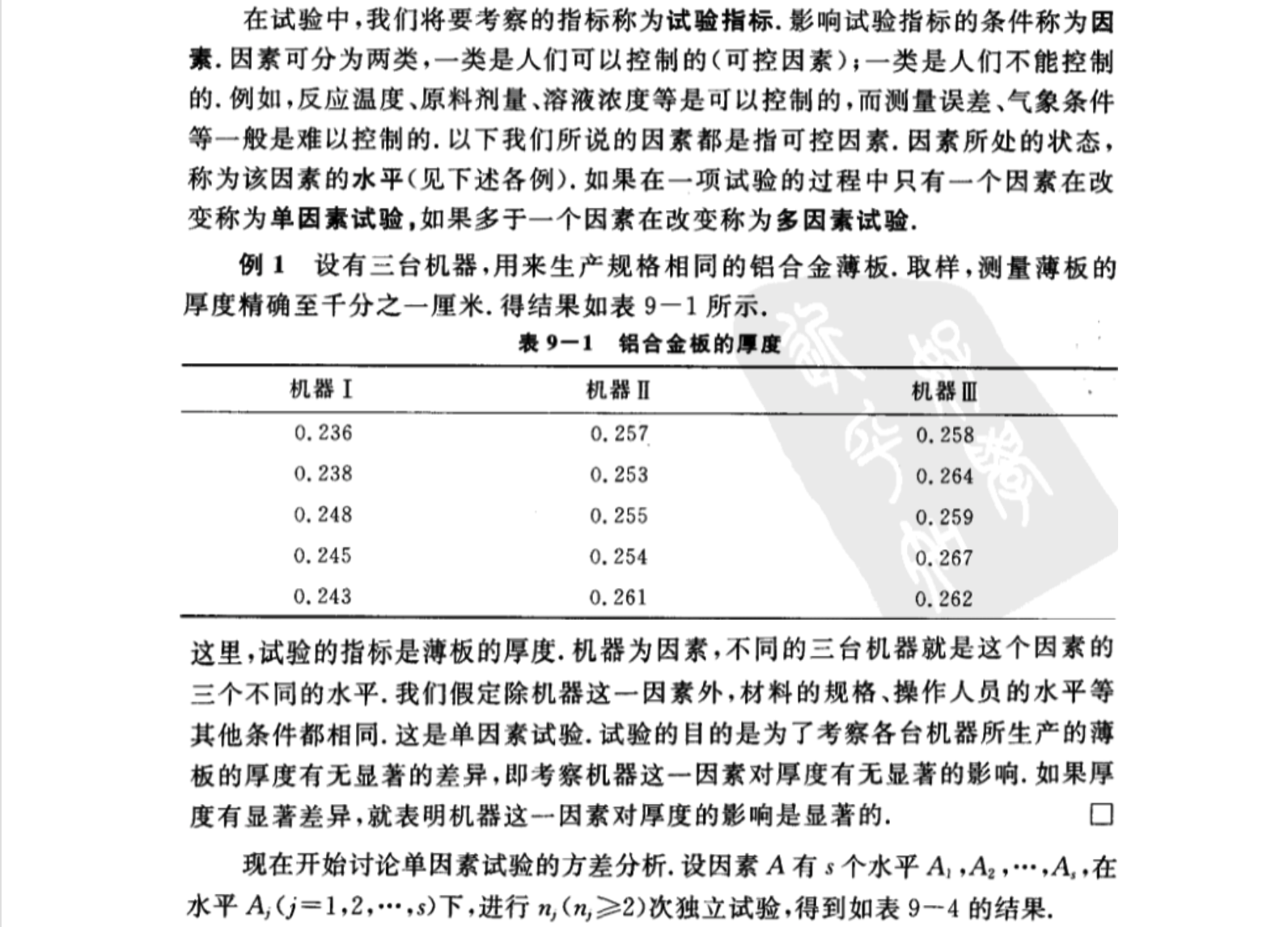


(二)平方和的分解

上述$S_E$的各项$(X_{ij}-\bar{X}{\cdot j})^2$表示在水平$A_j$下,样本观察值与样本均值的差异,这是由随机误差所引起的。$S_E$叫做误差平方和。$S_A$的各项$n_j(\bar{X}{\cdot j}-\bar{X})^2$表示$A_j$水平下的样本平均值与数据总平均值的差异,这是由水平$A_j$的效应的差异以及随机误差引起的。$S_A$叫做因素A的效应平方和。(1.8)式就是我们所需要的平方和分解式。
(三)SE,SA的统计特性


(四)假设检验问题的拒绝域


(五)未知参数估计
上面已讲过,不管H0是否为真,
$\hat{\sigma^2}=\frac{S_E}{n-s}$
是$\sigma^2$的无偏估计。

2 双因素方差分析表
(一)双因素等重复试验的方差分析





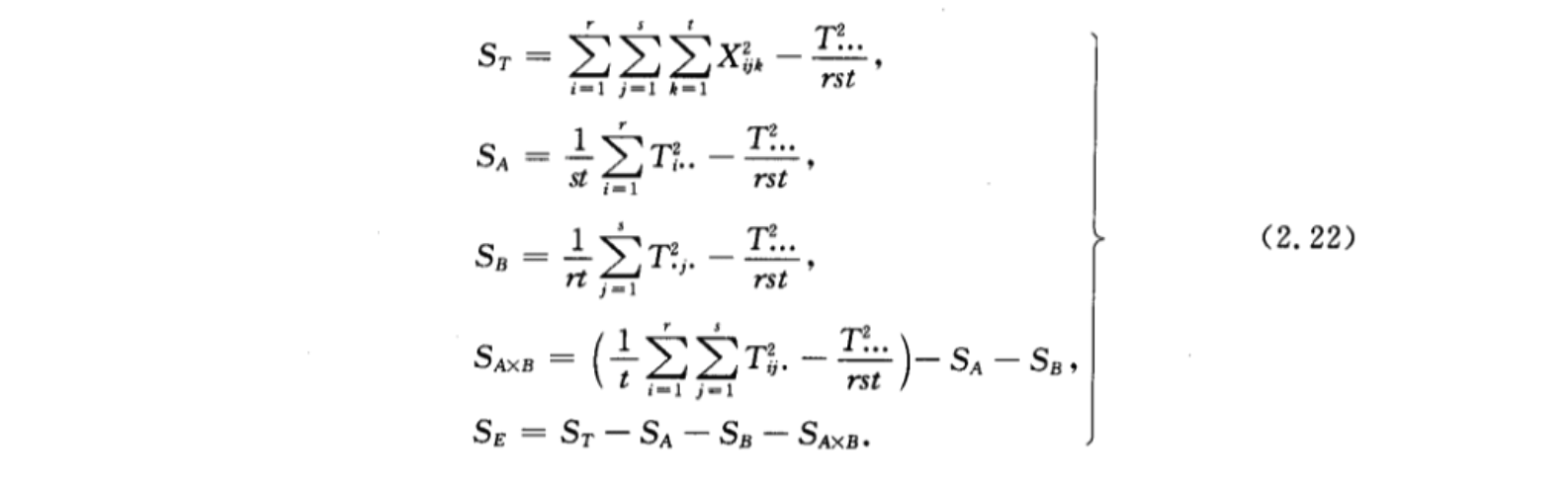
(二)双因素无重复试验的方差分析



3 一元线性回归
(一)一元线性回归

(二)a,b的估计



(三)σ2的估计


(四)线性假设的显著性检验


(五)系数b的置信区间

(六)回归函数μ(x)=ax+b函数值的点估计和置信区间

(七)Y的观察值的点预测和预测区间


(八)可化为一元线性回归的例子


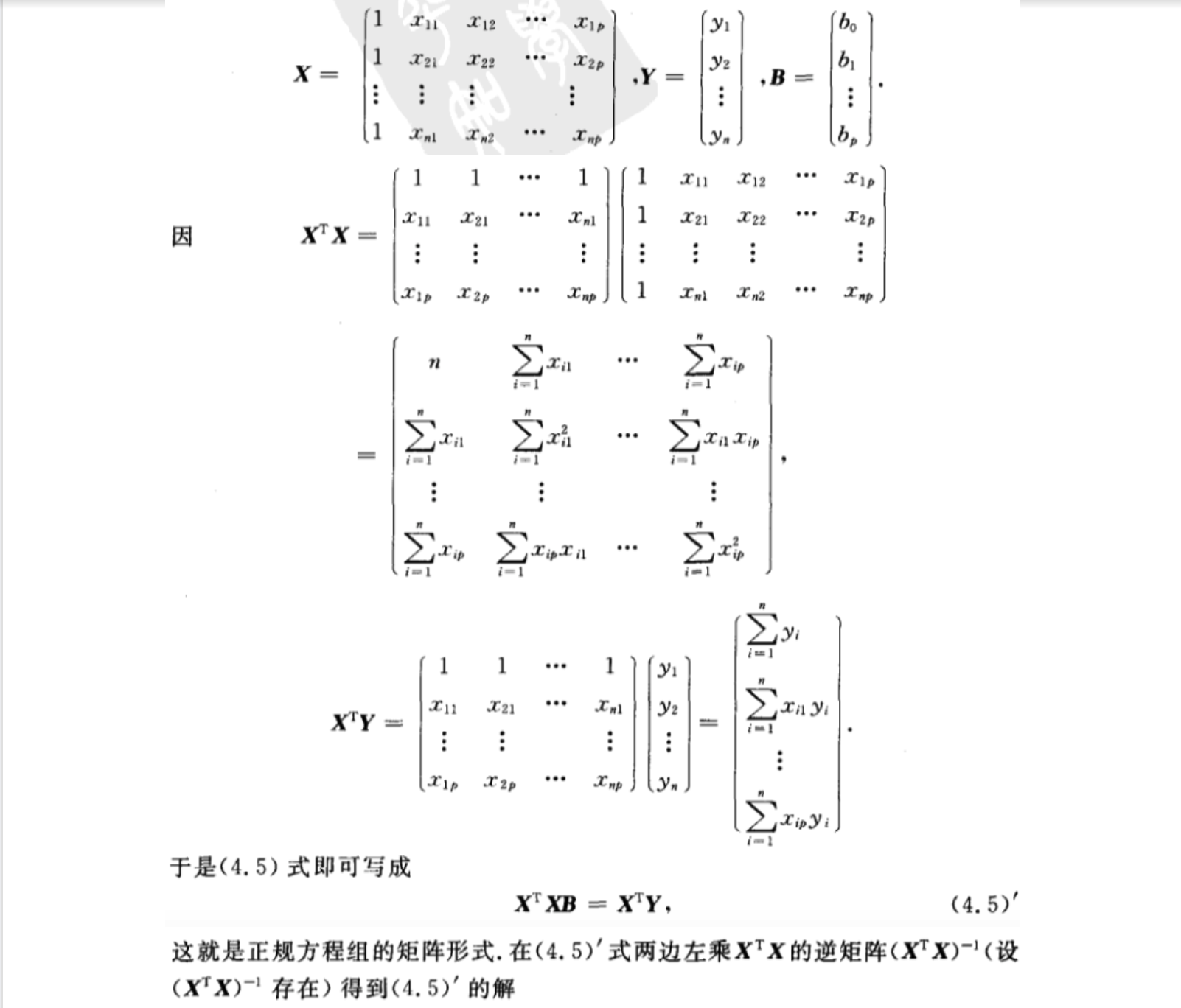
4 多元线性回归