第七章 参数估计
1 点估计

(一)矩估计法

(二)最大似然估计法


2 基于截尾样本的最大似然估计


3 估计量的评选标准

4 区间估计

5 正态总体均值和方差的区间估计
(一)单个总体N(μ,σ2)的情况
设已给定置信区间水平为$1-\alpha$,并设X1,X2,…,Xn为总体$N(\mu,\sigma^2)$的样本,$\bar{X},S^2$分别是样本均值和样本方差。
1 均值μ的置信区间
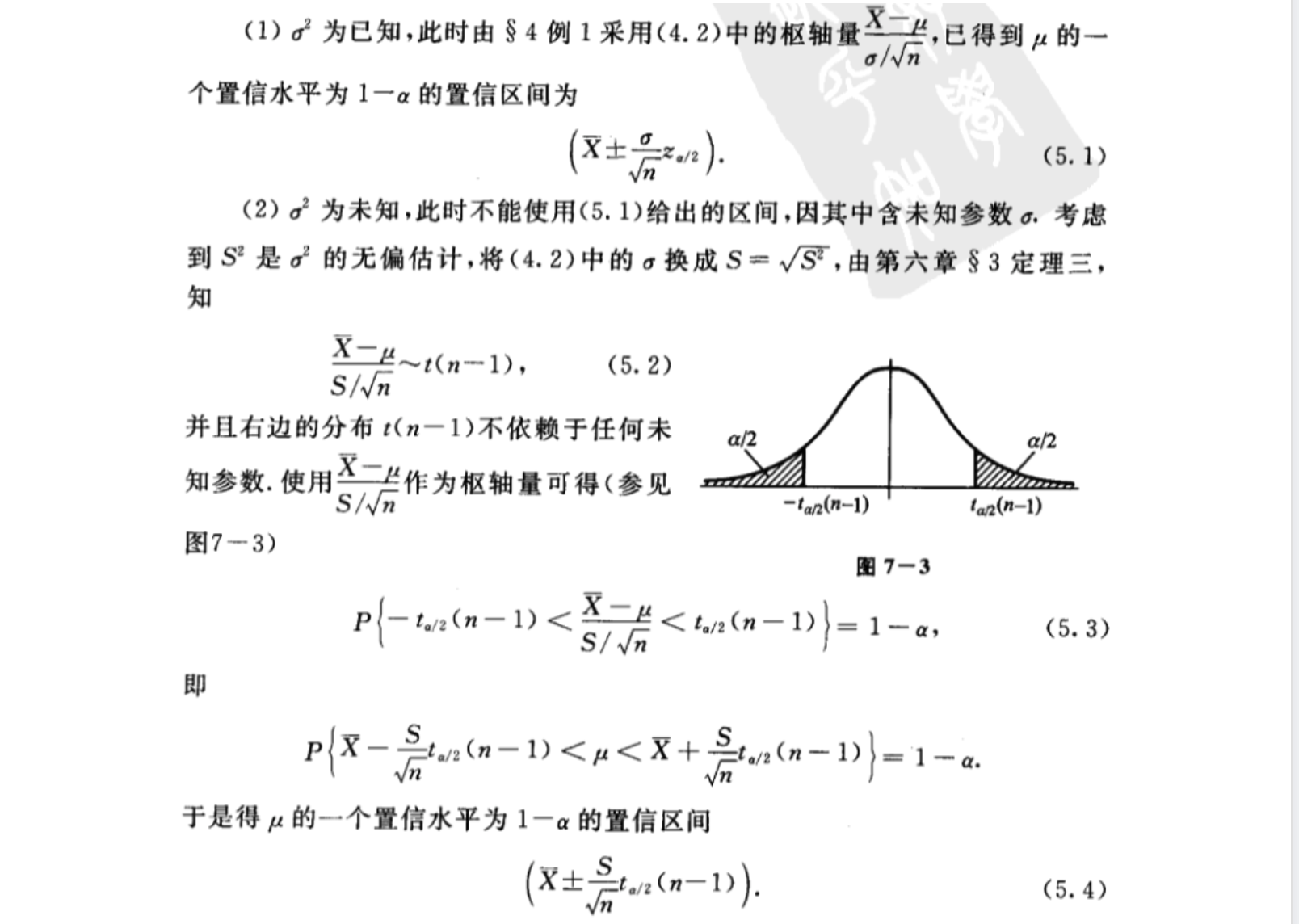
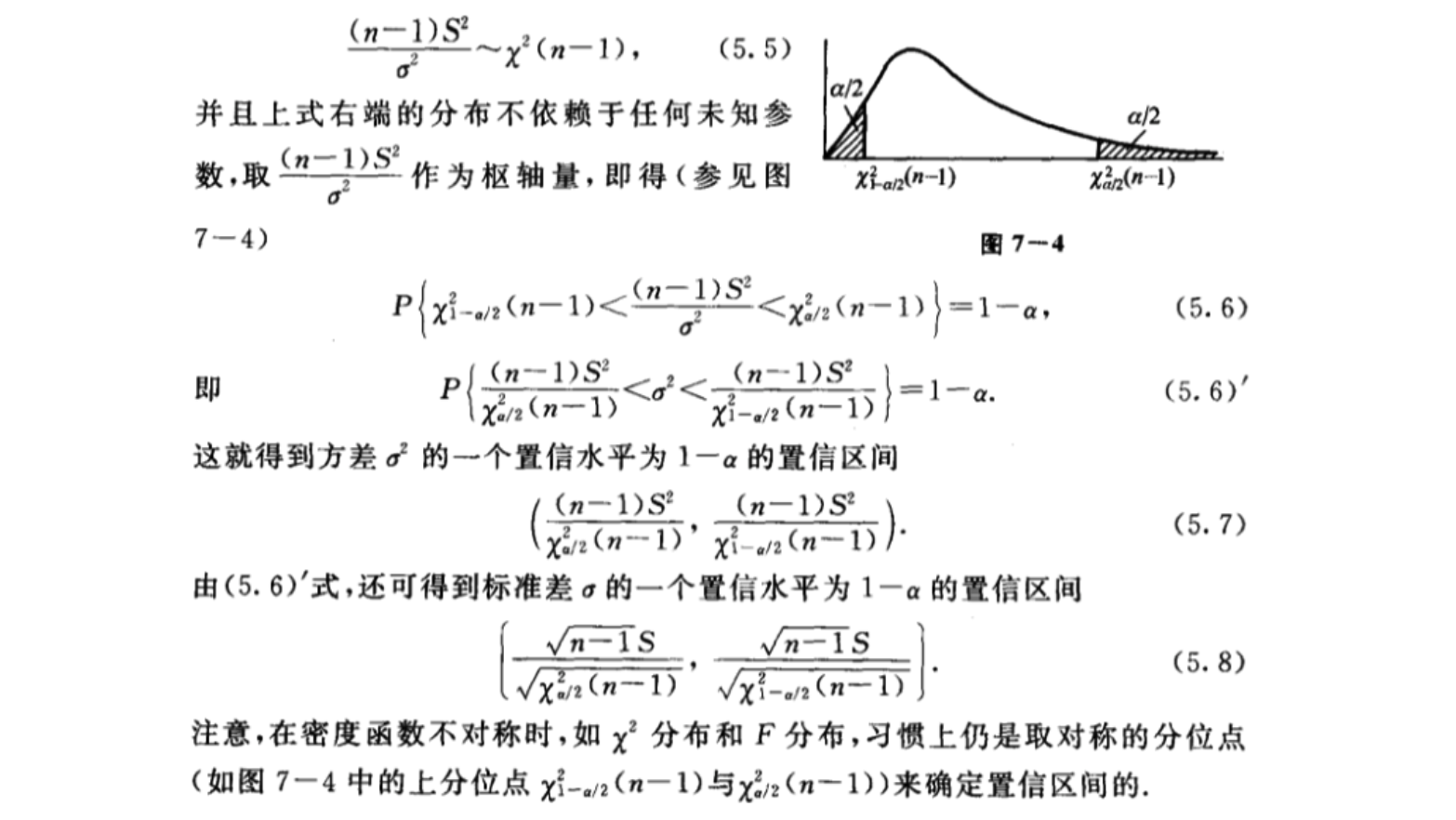
2 方差σ2的置信区间
此处,根据实际问题的需要,只介绍$\mu$未知的情况。$\sigma^2$的无偏估计为$S^2$,由第六章3定理二知:
(二)两个总体N(μ1,σ12),N(μ2,σ22)的情况
设已给定置信水平为$1-\alpha$,并设X1,X2,…,Xn是来自第一个总体的样本;Y1,Y2,…Yn是来自第二个总体的样本,这两个样本相互独立。且设$\bar{X},\bar{Y}$分别为第一、第二个总体的样本均值,$S^2_1,S^2_2$分别是第一、第二个总体的样本方差。
1 两个总体均值差μ1-μ2的置信区间

2 两个总体方差比的σ12/σ22置信区间

6 (0-1)分布参数的区间估计

7 单侧置信区间

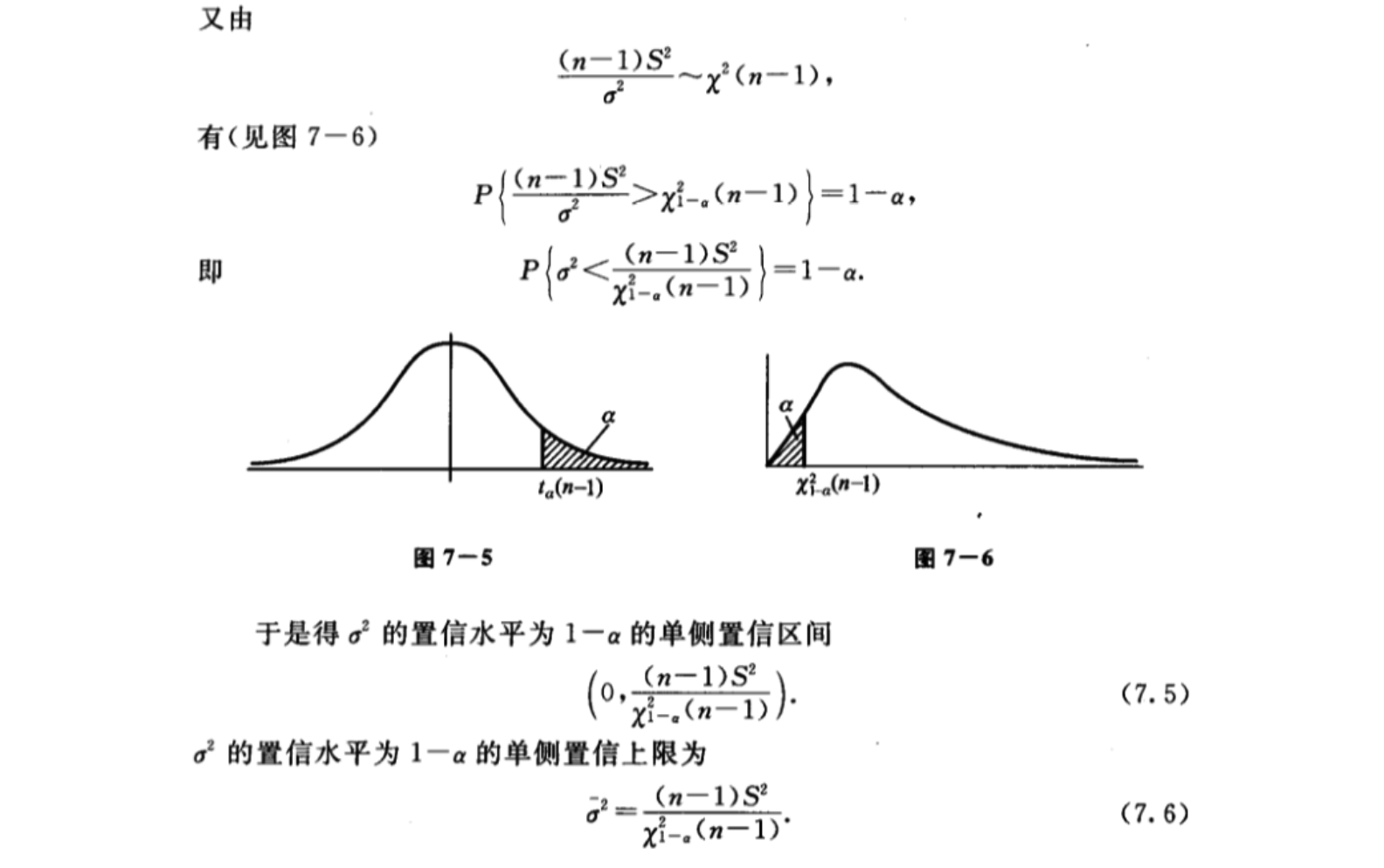
正态总体均值和方差的置信区间(置信水平为1-α)
