第二章 随机变量及其分布
1 随机变量
定义 设随机试验的样本空间为S={e}。X=X(e)是定义在样本空间S上的实值单值函数。称X=X(e)为随机变量。
2 离散型随机变量及其分布律

(一)(0-1)分布

(二)伯努利试验、二项分布

(三)泊松分布

泊松定理(泊松分布逼近二项分布)
泊松定理 设$\lambda>0$是一个常数,n是任意正整数,设$np_n=\lambda$,则对于任一固定的非负整数k,有
$lim_{n \to\infty}\binom{n}{k}p^k_n(1-p_n )^{n-k}=\frac{\lambda^k e^{-k}}{k!}$
3 随机变量的分布函数

4 连续型随机变量及其密度函数
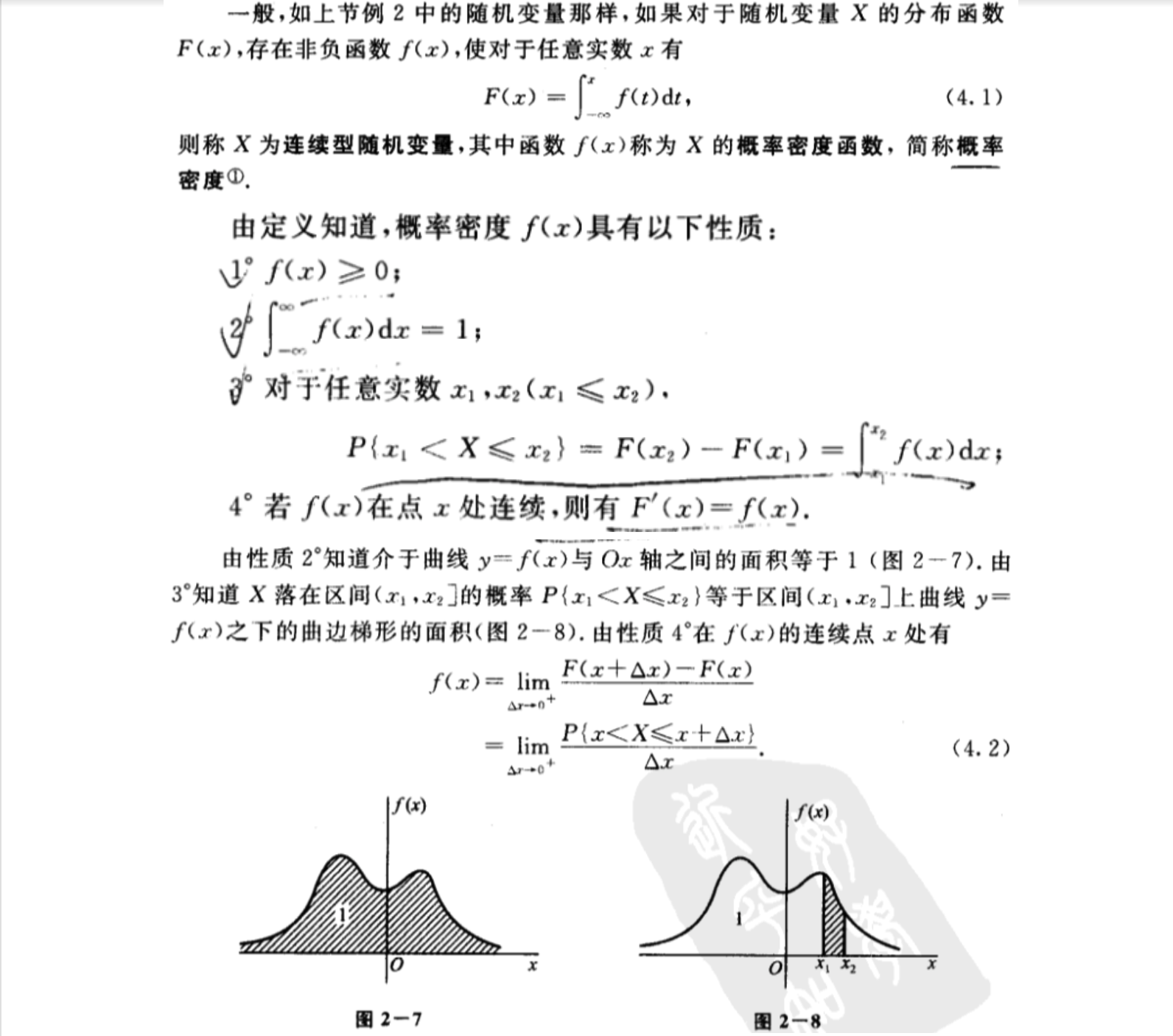
(一)均匀分布

(二)指数分布

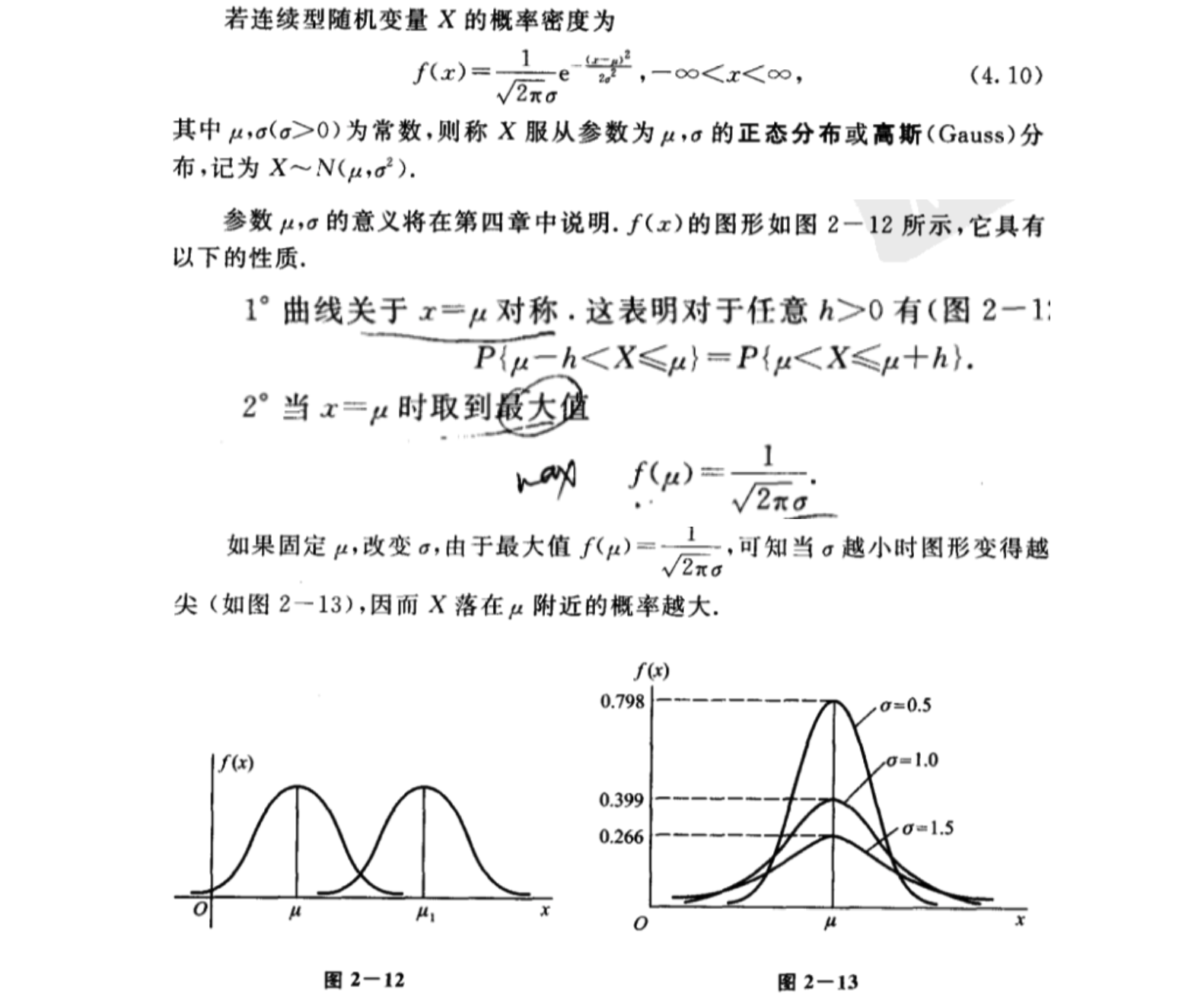
(三)正态分布
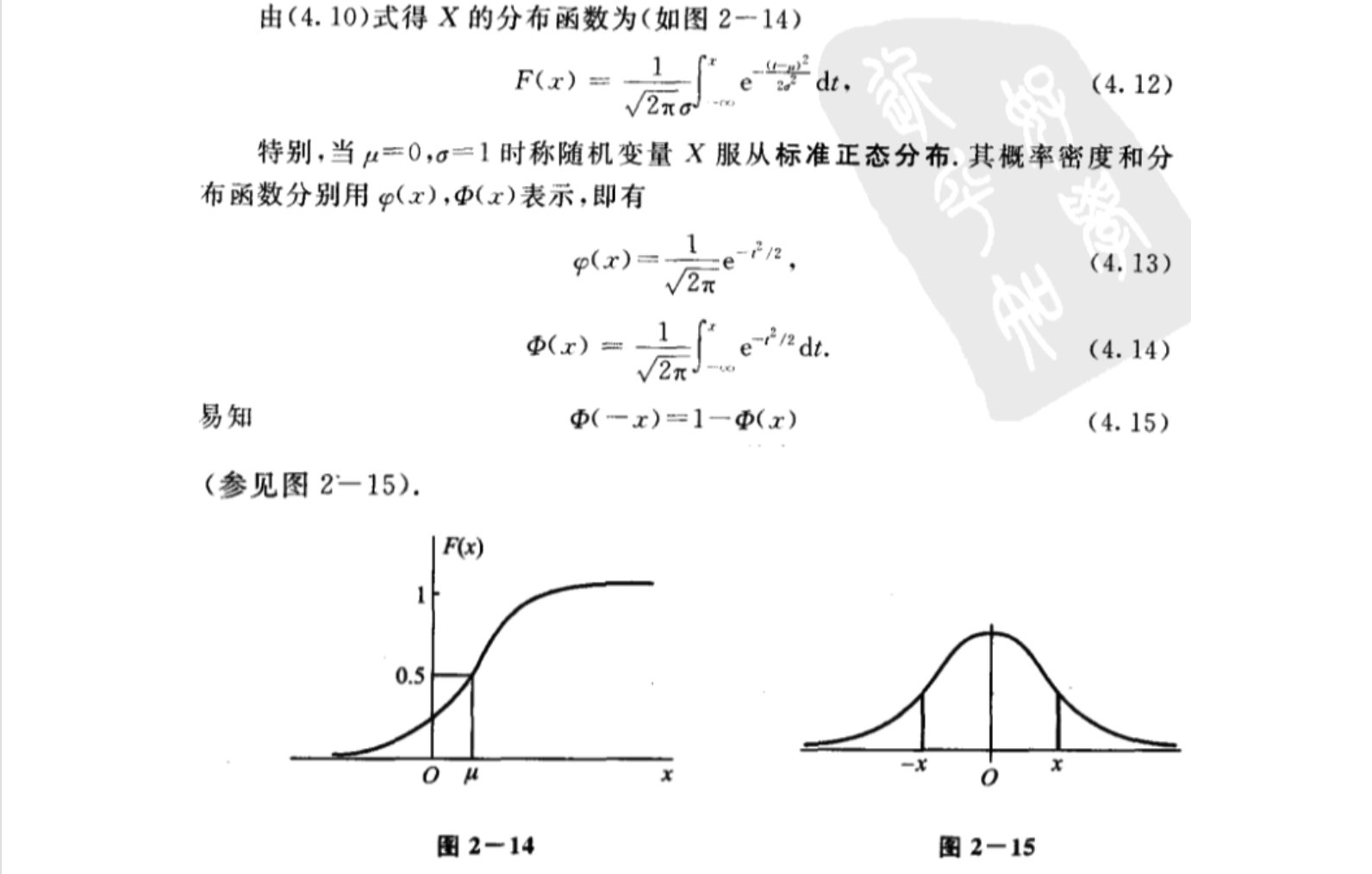
转换标准正态
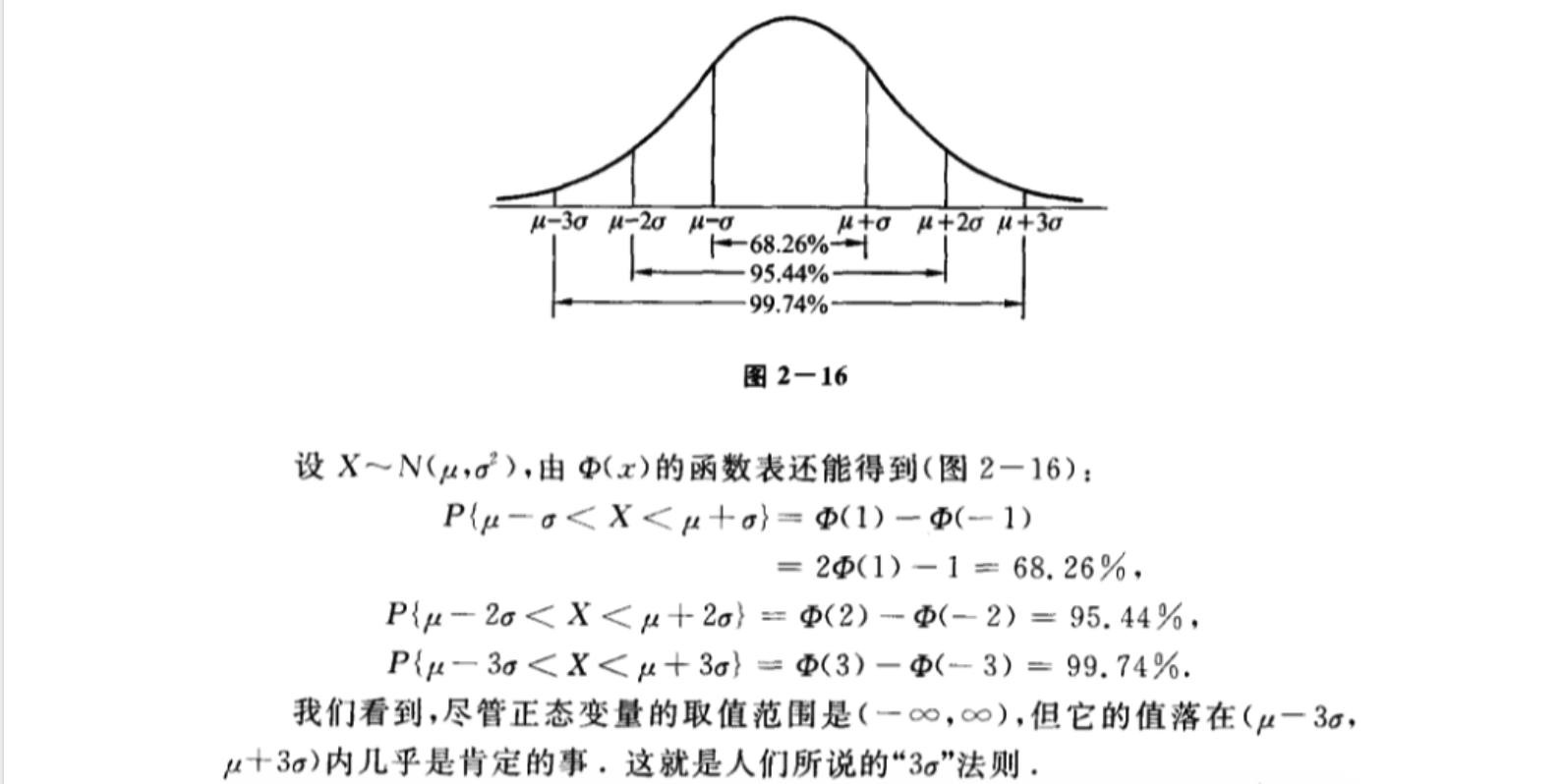
3σ法则
一般,若 $X \sim N(\mu,\sigma^2)$,我们只要通过一个线性变换就能将它化成标准正态分布。
引理 若$X \sim N(\mu,\sigma^2)$,则$Z=\frac{X-\mu}{\sigma}\sim N(0,1)$。
上α分位点

5 随机变量的函数的分布

(证明)转换标准正态分布
